Equations used in the solvers

Shallow-water equations

We consider a layered ocean with upward oriented z-axis:

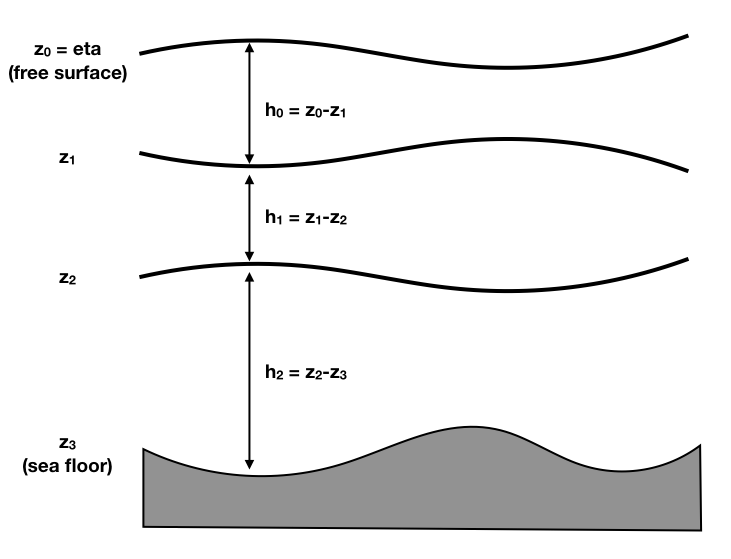
_images/nlayers.png

The adiabatic and non-dissipating shallow water equations for \(N\) layers can be written as

\[\mbox{D}_t \mathbf{u}_n = - \boldsymbol{\nabla} g m_n,\]
\[\partial_t h_n(x,y) + \boldsymbol{\nabla} \cdot (\mathbf{u}_n h_n ) = 0.\]

for \(n=0,\cdots, N-1\) (\(n=0\) corresponding to the top layer) and where \(\mathbf{u}_n\) and \(h_n\) are the layer 2d velocity and thickness, respectively, and \(g\) is the gravitational acceleration.

The normalized Montgomery potentials \(m_n = M_n / (g\rho_n)\) are proportional to the Montgomery potentials \(M_n\) and can be computed as \(m_0 = z_0\) and, for \(n>0\), as

\[m_n = \frac{\rho_{n-1}}{\rho_n} m_{n-1} + \left(1 - \frac{\rho_{n-1}}{\rho_n}\right) z_n.\]

Here \(\rho_n\) is the density in layer \(n\) and \(z_n\) is the \(z\)-coordinate of layer \(n\) upper boundary, given by:

\[ \begin{align}\begin{aligned}z_n &= z_{n-1} - h_{n-1},\\ &= - H(\mathbf{x}) + \sum_{j=n,N-1} h_j.\end{aligned}\end{align} \]

For example for \(N=2\), \(z_0 = - H(\mathbf{x}) + h_1 + h_0\) and \(z_1 = - H(\mathbf{x}) + h_1\). The total depth can be decomposed as the sum of a constant “full depth” \(\tilde H\) and a topography \(T(\mathbf{x})\) (the height of the submarine mountains), \(H(\mathbf{x}) = \tilde H - T(\mathbf{x})\), so that we find

\[\boldsymbol{\nabla} z_n = \boldsymbol{\nabla} \big(T + \sum_{j=n,N-1} h_j\big).\]

The equation for normalized Montgomery potential may be rewritten into a useful equation for interface vertical position:

\[z_n = \frac{\rho_n m_n -\rho_{n-1} m_{n-1}}{\rho_n - \rho_{n-1}}.\]

Note that since the velocity fields \(\mathbf{u}_n\) are not divergent-free, we have \(\mbox{D}_t \mathbf{u}_n = \partial_t \mathbf{u}_n + \boldsymbol{\nabla} |\mathbf{u}_n|^2/2 + \zeta_n \mathbf{e_z}\times \mathbf{u}_n\), with \(\zeta_n = \mathbf{e_z} \cdot (\boldsymbol{\nabla} \times \mathbf{u}_n )\) the relative vorticity.

Considering now Earth rotation, forcing, and, dissipating terms, the shallow water equation for conservation of momentum can be written as:

\[\partial_t \mathbf{u}_n(x,y) + (\zeta_n + f) \mathbf{e_z}\times\mathbf{u}_n = -\boldsymbol{\nabla} \Big \{ g (m_n + \Pi_n) + \frac{1}{2} |\mathbf{u}_n|^2 \Big \} + \mathbf{F}_{un} + \mathbf{D}(\mathbf{u}_n),\]

for \(n=0,\cdots, N-1\) and where:

  • \(f\) is the Coriolis frequency,

  • \(\Pi_n\) is a forcing potential, presumably tidal,

  • \(\mathbf{F}_{un}\) gathers non potential forcing (typically relaxations),

  • \(\mathbf{D}(\mathbf{u}_n)\) is dissipation.

The thickness tendency equation is:

\[\partial_t h_n(x,y) + \boldsymbol{\nabla} \cdot (\mathbf{u}_n h_n ) = F_{hn},\]

where \(F_{hn}\) represents thickness forcing and/or diabatic effects.

The pressure can be recomputed as:

\[p_n(x,y,z) = g \rho_n ( m_n(x,y) - z).\]

The one-layer case for N=1 is implemented in fluidsim.

Conserved quantities

We need to write the formula for the main quantities conserved by the equations.

  • kinetic energy:

\[E_k = \sum_{0,N-1} \frac{1}{2} \rho_n h_n |\mathbf{u}_n(x,y)|^2.\]

  • potential energy:

\[ \begin{align}\begin{aligned}E_p &= \sum_{0,N-1} \rho_n g \int_{z_{n+1}}^{z_n} z dz\\ &= \sum_{0,N-1} \frac{1}{2} \rho_n g (2z_{n+1} + h_n) h_n.\end{aligned}\end{align} \]

  • available potential energy:

\[E_{a} = \sum_{0,N-1} \frac{1}{2} \rho_n g (\eta_n^2 - \eta_{n+1}^2),\]

where \(\eta_n\) is the departure of the n’th interface from its position at rest.

  • potential enstrophy:

\[E_e = \sum_{0,N-1} \frac{1}{2} \rho_n \frac{(\zeta_n +f)^2}{h_n}.\]

Note that the potential vorticity is \(q_n=(\zeta_n+f)/h_n\)

Vertical normal modes

We assume now the layers are weakly departing from a rest state characterized by layer thicknesses \(H_n\) and associated interface vertical positions \(Z_n\). We also assume the topography is flat. Interface displacement from their positions at rest are labelled \(\eta_n\), such that:

\[z_n = Z_n + \eta_n\]

The temporal evolution of layer thicknesses is then given by:

\[\partial_t h_n(x,y) + H_n \boldsymbol{\nabla} \cdot \mathbf{u}_n = F_h.\]

One can then separate vertical and horizontal dependencies according to:

\[ \begin{align}\begin{aligned}u_n &= u(x,y,t) \phi_n\\m_n &= m(x,y,t) \phi_n\\h_n &= h(x,y,t) \times \lambda \phi_n H_n\end{aligned}\end{align} \]

The vertical mode structure functions \(\phi_n\) satisfy the following eigenvalue problem:

\[\lambda \phi_n H_n = -\frac{\rho_{n-1}}{\rho_{n}-\rho_{n-1}} \phi_{n-1} + \Big \{ \frac{\rho_{n-1}}{\rho_{n}-\rho_{n-1}} + \frac{\rho_{n}}{\rho_{n+1}-\rho_{n}} \Big \} \phi_n - \frac{\rho_{n}}{\rho_{n+1}-\rho_{n}} \phi_{n},\]

for \(0<n<N-1\), and:

\[ \begin{align}\begin{aligned}\lambda \phi_0 H_0 = \phi_0 - \frac{\rho_{1} \phi_1 - \rho_{0} \phi_0}{\rho_{1}-\rho_{0}},\\\lambda \phi_{N-1} H_{N-1} = \frac{\rho_{N-1} \phi_{N-1} - \rho_{N-2} \phi_{N-2}}{\rho_{N-1}-\rho_{N-2}},\end{aligned}\end{align} \]

The eigenvalue if related to an equivalent speed \(c_n\) according \(c_n=\sqrt{g/\lambda}\)

Quasi-geostrophic equations

We consider now that the flow weakly depart from a reference state given by constant and uniform layer thicknesses \(H_n\).

Each interface is departing from its mean position by \(\eta_n\). The layer thickness is then given by \(h_n=H_n+\eta_{n}-\eta_{n+1}\).

Normalized Montgomery potentials anomaly are then given by \(\mu_0 = \eta_0\) and for \(n>0\) as:

\[\mu_n = \frac{\rho_{n-1}}{\rho_n} \mu_{n-1} - \left(1 - \frac{\rho_{n-1}}{\rho_n}\right) \eta_n.\]

This last expression can be rewritten to express \(\eta_n\) as a function of \(\mu\)’s:

\[ \begin{align}\begin{aligned}\eta_n &= \frac{\rho_n \mu_n - \rho_{n-1} \mu_{n-1}}{\rho_n - \rho_{n-1}},\\ &\sim \frac{\rho_n}{\rho_n - \rho_{n-1}} \times (\mu_n - \mu_{n-1}),\end{aligned}\end{align} \]

where the last approximation will be considered as an equality next.

Under typical quasi-geostrophic conditions (weak Rossby number, weak topography), the flow is at zeroth order geostrophic:

\[\mathbf{u}_n = \mathbf{e_z} \cdot \boldsymbol{\nabla} \big \{ g \mu_n/f_0 \big \}.\]

The geostrophic streamfunction is thus \(\psi_n=g \mu_n/f_0\).

The curl of momentum conservation is at first order given by:

\[\mbox{D}_t \big \{ \zeta_n+f' \big \} + f_0 \boldsymbol{\nabla}\cdot\mathbf{u}_n = \boldsymbol{\nabla} \times \big \{ \mathbf{F}_{un} + \mathbf{D}(\mathbf{u}_n) \big \},\]

where \(f'=f-f_0\).

The divergence of the horizontal flow is given by the thickness tendency equation:

\[ \begin{align}\begin{aligned}\boldsymbol{\nabla}\cdot\mathbf{u}_n &= -\mbox{D}_t h_n/H_n + F_{hn}/H_n,\\ &= \mbox{D}_t ( \eta_{n}-\eta_{n-1} )/H_n + F_{hn}/H_n,\end{aligned}\end{align} \]

which leads to the conservation of QG potential vorticity:

\[\mbox{D}_t q_n = \boldsymbol{\nabla} \times \big \{ \mathbf{F}_{un} + \mathbf{D}(\mathbf{u}_n) \big \} - f_0 F_{hn}/H_n .\]

where \(q_n\) is the quasi-geostrophic potential vorticity:

\[q_n = \zeta_n + f' + f_0 ( \eta_{n}-\eta_{n-1} )/H_n,\]

For interior layers (\(0<n<N-1\)):

\[q_n = \nabla^2 \psi_n + f' + \frac{f_0^2}{H_n} \Big \{ \frac{\psi_n - \psi_{n-1}}{g_n'} - \frac{\psi_{n-1} - \psi_{n-2}}{g_{n-1}'} \Big \}\]

where \(g_n'=g(\rho_n - \rho_{n-1})/\rho_n\).

Forcing: waves

We want to force internal waves with a given frequency \(\omega\) and modal vertical structure corresponding to mode f. The forcing required to do that, while not producing spurious QG potential vorticity, should look like:

\[ \begin{align}\begin{aligned}\mathbf{F}_{un} = (f_u, f_v) h(x,y, t) \phi_{f,n},\\\mathbf{F}_{hn} = (f_v \partial_x h - f_u \partial_y h) \; f_0 H_n \phi_{f,n},\end{aligned}\end{align} \]

where (\(f_u\), \(f_v\)) are constants, \(h(x,y)\) describes the horizontal spatial and temporal structure of the forcing, \(\phi_f\) is the \(f\) vertical mode number. The spatiotemporal structure is chosen to match that of the expected wave, i.e. a sinusoidal-like shape with wave number \(k\) satisfying the following dispersion relationship

\[\omega^2 = f^2 + c_f^2 k^2.\]

In general: \(h=\sin[ k (y-y_c)-\omega t]\)

A dirac in y and spatial uniformity in x may also work.

Forcing: vortices

In order to force a turbulent eddy field, we apply a forcing that looks like:

\[ \begin{align}\begin{aligned}\mathbf{F}_{un} = f_{uv} (-\partial_y h, \partial_x h ) \phi_{f,n} ,\\\mathbf{F}_{hn} = f_h h(x,y,t) \frac{g H_n}{c_f^2} \phi_{f,n}.\end{aligned}\end{align} \]

where the spatial and temporal structure of the forcing is given by:

\[h(x,y,t) = s \Big [(x - x_c) \cos(\omega t) + (y-y_c) \sin(\omega t) \Big ],\]

where \(s\) is a smoothly varying step function. The QG potential vorticity will be generated at the following rate:

\[\mbox{D}_t q_n = \Big \{ f_{uv} \nabla^2 h - f_h h \frac{gf}{c_f^2} \Big \} \phi_{f,n}\]

We choose for now \(f_{uv}=0\).